论文原文《A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II》,可在IEEE上搜索。
简要叙述:编码交叉变异依然不变,在在此基础上加上了
- 快速非支配排序
- 拥挤度
- 精英策略
非支配排序
支配简述:对于一个点a,他的f1(a), f2(a)……fn(a)都比另一个点b,他的f1(b), f2(b)……fn(b)大,那么a支配b。
非支配即a他的所有值至少有一个小于b,且至少有一个大于b,那么,那么a和b非支配。
NSGA-ii 使用快速非支配排序,具体算法可见代码,根据代码思路自己去画一画。
非支配排序会最终将很多点分成不同rank的类,根据目标所需最大最小不同后续选择对rank不同的排序。
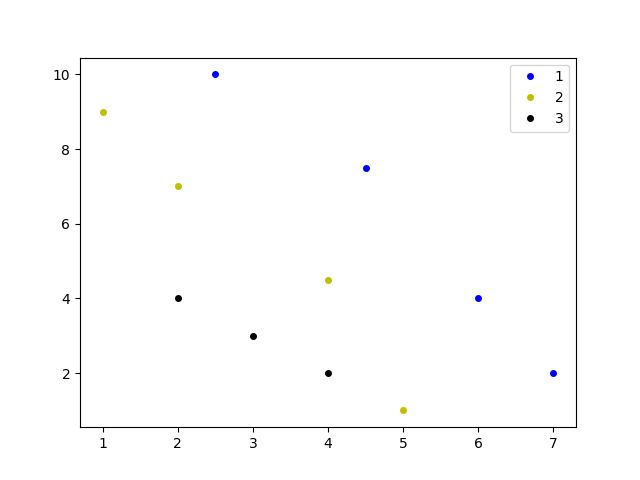
例子代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import matplotlib.pyplot as plt import numpy as np P = np.array([[1, 9], [2, 7], [3, 3], [2.5, 10], [4, 4.5], [5, 1], [4.5, 7.5], [6, 4], [7, 2], [2, 4], [4, 2]]) def fast_non_dominated_sort(values1, values2): S = [[] for i in range(0, len(values1))] front = [[]] n = [0 for i in range(0, len(values1))] rank = [0 for i in range(0, len(values1))] for p in range(0, len(values1)): S[p] = [] n[p] = 0 for q in range(0, len(values1)): if (values1[p] > values1[q] and values2[p] > values2[q]) or (values1[p] >= values1[q] and values2[p] > values2[q]) or ( values1[p] > values1[q] and values2[p] >= values2[q]): if q not in S[p]: S[p].append(q) elif (values1[q] > values1[p] and values2[q] > values2[p]) or (values1[q] >= values1[p] and values2[q] > values2[p]) or ( values1[q] > values1[p] and values2[q] >= values2[p]): n[p] = n[p] + 1 if n[p] == 0: rank[p] = 0 if p not in front[0]: front[0].append(p) print(S, n) i = 0 while front[i] != []: Q = [] for p in front[i]: for q in S[p]: n[q] = n[q] - 1 if n[q] == 0: rank[q] = i + 1 if q not in Q: Q.append(q) i = i + 1 front.append(Q) del front[len(front) - 1] return front ans = fast_non_dominated_sort(P[:, 0], P[:, 1]) plt.plot([P[i, 0] for i in ans[0]], [P[i, 1] for i in ans[0]], "b.", markersize=8, label="1") plt.plot([P[i, 0] for i in ans[1]], [P[i, 1] for i in ans[1]], "y.", markersize=8, label="2") plt.plot([P[i, 0] for i in ans[2]], [P[i, 1] for i in ans[2]], "k.", markersize=8, label="3") plt.legend() plt.show() |
拥挤度计算
个人认为很多时候可以用用拥挤距离替代,每个类都分别计算拥挤度,但最终很多时候在算法中只需要计算一个rank的拥挤度。
一个rank中的所有点,其中第一个点和最后一个点的拥挤距离为∞,中间点的距离即delta_y1 + delta_y2。拥挤距离可用delta_y1 / (max(y1) – min(y1)) + delta_y2 / (max(y2) – min(y2))
精英策略
每次从n个种群交叉变异后会生成2n的种群,通过精英策略选取其中前n个进行下一次迭代。策略如下:
- rank大/小的优先,看具体题目
- 如果有个rank加上后在超过了n个个体的种群,则进行拥挤度排序,选取最大/小的直到种群为n个个体。
Github上大佬的代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 |
# Program Name: NSGA-II.py # Description: This is a python implementation of Prof. Kalyanmoy Deb's popular NSGA-II algorithm # Author: Haris Ali Khan # Supervisor: Prof. Manoj Kumar Tiwari # Importing required modules import math import random import matplotlib.pyplot as plt # First function to optimize def function1(x): # value = -x ** 2 value = x * math.sin(10 * math.pi * x) + 2 return value # Second function to optimize def function2(x): # value = -(x - 2) ** 2 value = 1 return value # Function to find index of list def index_of(a, list): for i in range(0, len(list)): if list[i] == a: return i return -1 # Function to sort by values def sort_by_values(list1, values): sorted_list = [] while len(sorted_list) != len(list1): if index_of(min(values), values) in list1: sorted_list.append(index_of(min(values), values)) values[index_of(min(values), values)] = math.inf return sorted_list # Function to carry out NSGA-II's fast non dominated sort def fast_non_dominated_sort(values1, values2): S = [[] for i in range(0, len(values1))] front = [[]] n = [0 for i in range(0, len(values1))] rank = [0 for i in range(0, len(values1))] for p in range(0, len(values1)): S[p] = [] n[p] = 0 for q in range(0, len(values1)): if (values1[p] > values1[q] and values2[p] > values2[q]) or (values1[p] >= values1[q] and values2[p] > values2[q]) or ( values1[p] > values1[q] and values2[p] >= values2[q]): if q not in S[p]: S[p].append(q) elif (values1[q] > values1[p] and values2[q] > values2[p]) or (values1[q] >= values1[p] and values2[q] > values2[p]) or ( values1[q] > values1[p] and values2[q] >= values2[p]): n[p] = n[p] + 1 if n[p] == 0: rank[p] = 0 if p not in front[0]: front[0].append(p) i = 0 while front[i] != []: Q = [] for p in front[i]: for q in S[p]: n[q] = n[q] - 1 if n[q] == 0: rank[q] = i + 1 if q not in Q: Q.append(q) i = i + 1 front.append(Q) del front[len(front) - 1] return front # Function to calculate crowding distance def crowding_distance(values1, values2, front): distance = [0 for i in range(0, len(front))] sorted1 = sort_by_values(front, values1[:]) sorted2 = sort_by_values(front, values2[:]) distance[0] = 0x6f6f6f6f distance[len(front) - 1] = 0x6f6f6f6f for k in range(1, len(front) - 1): distance[k] = distance[k] + (values1[sorted1[k + 1]] - values1[sorted1[k - 1]]) / (max(values1) - min(values1)) for k in range(1, len(front) - 1): distance[k] = distance[k] + (values2[sorted2[k + 1]] - values2[sorted2[k - 1]]) / (max(values2) - min(values2)) return distance # Function to carry out the crossover def crossover(a, b): r = random.random() if r > 0.5: return mutation((a + b) / 2) else: return mutation((a - b) / 2) # Function to carry out the mutation operator def mutation(solution): mutation_prob = random.random() if mutation_prob < 1: solution = min_x + (max_x - min_x) * random.random() return solution # Main program starts here pop_size = 20 max_gen = 100 # Initialization min_x = -1 max_x = 2 solution = [min_x + (max_x - min_x) * random.random() for i in range(0, pop_size)] gen_no = 0 while gen_no < max_gen: function1_values = [function1(solution[i]) for i in range(0, pop_size)] function2_values = [function2(solution[i]) for i in range(0, pop_size)] non_dominated_sorted_solution = fast_non_dominated_sort(function1_values[:], function2_values[:]) print("The best front for Generation number ", gen_no, " is") for valuez in non_dominated_sorted_solution[0]: print(round(solution[valuez], 3), end=" ") print("\n") crowding_distance_values = [] for i in range(0, len(non_dominated_sorted_solution)): crowding_distance_values.append(crowding_distance(function1_values[:], function2_values[:], non_dominated_sorted_solution[i][:])) solution2 = solution[:] # Generating offsprings while len(solution2) != 2 * pop_size: a1 = random.randint(0, pop_size - 1) b1 = random.randint(0, pop_size - 1) solution2.append(crossover(solution[a1], solution[b1])) function1_values2 = [function1(solution2[i]) for i in range(0, 2 * pop_size)] function2_values2 = [function2(solution2[i]) for i in range(0, 2 * pop_size)] non_dominated_sorted_solution2 = fast_non_dominated_sort(function1_values2[:], function2_values2[:]) crowding_distance_values2 = [] for i in range(0, len(non_dominated_sorted_solution2)): crowding_distance_values2.append(crowding_distance(function1_values2[:], function2_values2[:], non_dominated_sorted_solution2[i][:])) new_solution = [] for i in range(0, len(non_dominated_sorted_solution2)): non_dominated_sorted_solution2_1 = [index_of(non_dominated_sorted_solution2[i][j], non_dominated_sorted_solution2[i]) for j in range(0, len(non_dominated_sorted_solution2[i]))] front22 = sort_by_values(non_dominated_sorted_solution2_1[:], crowding_distance_values2[i][:]) front = [non_dominated_sorted_solution2[i][front22[j]] for j in range(0, len(non_dominated_sorted_solution2[i]))] front.reverse() for value in front: new_solution.append(value) if len(new_solution) == pop_size: break if len(new_solution) == pop_size: break solution = [solution2[i] for i in new_solution] gen_no = gen_no + 1 # Lets plot the final front now print(solution[0]) print(function1(solution[0])) function1 = [i * -1 for i in function1_values] function2 = [j * -1 for j in function2_values] plt.xlabel('Function 1', fontsize=15) plt.ylabel('Function 2', fontsize=15) plt.scatter(function1, function2) plt.show() |
 浙公网安备 33010902002953号
浙公网安备 33010902002953号